こんにちは、しらすです。
今回は機械学習を行うにあたってふと疑問に思った「損失関数と精度の違い」について、回帰問題と分類問題の観点から述べたいと思います。
回帰問題と分類問題とは
まずは回帰問題と分類問題ってそれぞれ何??という疑問から簡単に述べておきます。
連続的な値(値段など)を予測するものを回帰問題、離散的で順番に意味を持たないもの(花の種類など)を予測するものを分類問題と言います。
精度と損失関数は、回帰問題の場合は同じですが、分類問題の場合は別と考えられます。
回帰問題における精度と損失関数
連続的に値が変化する回帰問題の場合、正解値との差を算出する損失関数がそのまま同じく精度となります。
代表的な損失関数
平均二乗誤差 / Mean Squared Error
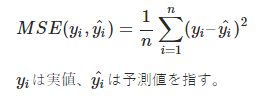
外れ値に対する感度が高い。
平均絶対誤差 / Mean Absolute Error
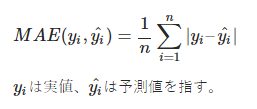
外れ値に対する感度が低い(変に影響されない)
平均二乗対数誤差 / Mean Squared Logarithmic Error
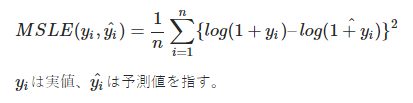
予測が実値を上回りやすくなるという傾向がある
分類問題における精度と損失関数
種類を分類する分類問題の場合、正解 or 不正解で正解率で評価する精度と、不正解の場合どの程度不正解だったかで評価する損失関数では意味が異なります。
3クラスに分類する場合
例えば3つのクラス(A,B,C)に分類する問題の場合の精度と損失関数について考えます。
正解がAのデータを以下のように間違えて予測したとします。
- A:20%
- B:50%
- C:30%
この結果はBと選択されたため、精度としては単純に不正解となるが、損失関数としては不正解の度合いが算出できます。
代表的な損失関数
交差エントロピー誤差 / cross entropy error

モデルで写真を判定してみると犬である確率は20%、猫である確率30%、馬である確率が50%であると予測しました。この写真が馬であったとしましょう。この時、クロスエントロピー誤差はいくつになるでしょうか。以下のように求まります。
E=–(0×log0.2+0×log0.3+1×log0.5)=–log0.5
https://ai-trend.jp/basic-study/neural-network/nn_loss_function/
分類問題ではほとんどがこの交差エントロピーを使用します。
正解のカテゴリーをうまく予測すると交差エントロピー誤差も小さくなります。ディープラーニングやニューラルネットなどで分類問題を解くときにも使用されます。
参考
機械学習における損失関数の役割や種類についてはこちら
交差エントロピーについてこちらではもう少し細かく考察されております。分類問題で誤差二乗を使うこともできるのですが、交差エントロピーを使うことで学習速度が向上する様子。

Kerasで使える損失関数はこちらから。





コメント